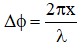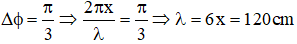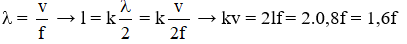- Lớp học
- Kiểm Tra
- Thi đấu
- Ôn thi TN THPT
- Ôn thi tốt nghiệp THPT môn Toán - Lớp 12
- Ôn thi tốt nghiệp THPT môn Ngữ văn - Lớp 12
- Ôn thi tốt nghiệp THPT môn Vật lý- Lớp 12
- Ôn thi tốt nghiệp THPT môn Hoá học - Lớp 12
- Ôn thi tốt nghiệp THPT môn Sinh học - Lớp 12
- Ôn thi tốt nghiệp THPT môn Lịch sử - Lớp 12
- Ôn thi tốt nghiệp THPT môn Địa lý - Lớp 12
- Ôn thi Tốt nghiệp THPT môn Giáo dục Kinh tế Pháp luật - Lớp 12
- Mua thẻ VIP
- VinaPhone

Bài tập
Câu hỏi số 1/20
17:03
Điểm: 0
trên tổng số 100
Góp ý - Báo lỗi
Điểm của bạn.Mỗi câu trả lời đúng được
Câu hỏi này theo dạng chọn đáp án đúng, sau khi đọc xong câu hỏi, bạn bấm vào một trong số các đáp án mà chương trình đưa ra bên dưới, sau đó bấm vào nút gửi để kiểm tra đáp án và sẵn sàng chuyển sang câu hỏi kế tiếp
| Trong khoảng 5 phút đầu tiên | + 5 điểm |
| Trong khoảng 5 phút -> 10 phút | + 4 điểm |
| Trong khoảng 10 phút -> 15 phút | + 3 điểm |
| Trong khoảng 15 phút -> 20 phút | + 2 điểm |
| Trên 20 phút | + 1 điểm |
Tổng thời gian làm mỗi câu (không giới hạn)
Điểm của bạn.
Bấm vào đây nếu phát hiện có lỗi hoặc muốn gửi góp ý
×
Em chưa làm xong câu này
Em có muốn tiếp tục làm không?
Bỏ qua
Làm tiếp

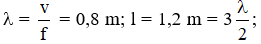
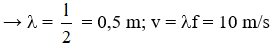
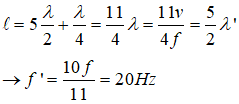
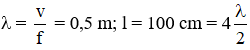
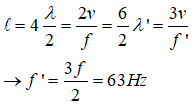
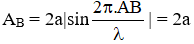
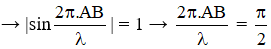
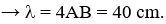

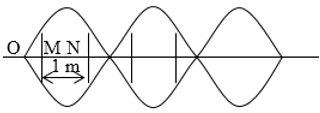
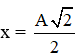 Δt = T/4
Δt = T/4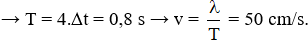
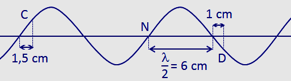
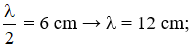
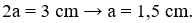
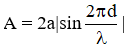
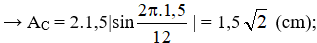

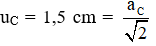 và hướng về vị trí cân bằng nên
và hướng về vị trí cân bằng nên 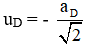 và cũng hướng về vị trí cân bằng.
và cũng hướng về vị trí cân bằng.
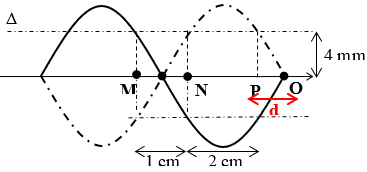
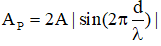 thay số
thay số