Bài 14: Mạch có R, L, C mắc nối tiếp - Vật lý lớp 12

Điện áp và tổng trở của mạch: 

$U=\sqrt{U_{R}^{2}+{{({{U}_{L}}-{{U}_{C}})}^{2}}}$

$Z=\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}$

Định luật Ohm cho mạch: 

$I=\frac{U}{Z}=\frac{\sqrt{U_{R}^{2}+{{({{U}_{L}}-{{U}_{C}})}^{2}}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}=\frac{{{U}_{R}}}{R}=\frac{{{U}_{L}}}{{{Z}_{L}}}=\frac{{{U}_{C}}}{{{Z}_{C}}}=\frac{{{I}_{0}}}{\sqrt{2}} $

Độ lệch pha của điện áp và cường độ dòng điện trong mạch là $φ$, được cho bởi: $\tan \varphi =\frac{{{U}_{L}}-{{U}_{C}}}{{{U}_{R}}}=\frac{{{Z}_{L}}-{{Z}_{C}}}{R}$; $φ=φ_u−φ_i$

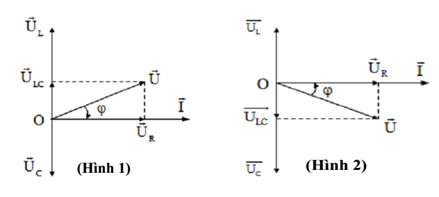
- Khi $U_L>U_C$ hay $Z_L>Z_C$thì u nhanh pha hơn i góc $φ$. (Hình 1). Khi đó ta nói mạch có tính cảm kháng.

- Khi $U_C>U_L$ hay $Z_C>Z_L$ thì u chậm pha hơn i góc $φ$. (Hình 2). Khi đó ta nói mạch có tính dung kháng.

 Giản đồ véc tơ (Giản đồ Frenen):